「07」倍增应用 - ST 算法
ST 表
ST 表(Sparse Table,稀疏表)是一种用于解决 RMQ(Range Minimum/Maximum Query,区间最值问题) 的经典数据结构。
它的核心思想是预处理和倍增。虽然它在预处理后不支持在线修改(属于静态数据结构),但在查询效率上达到了极致。
1. 核心应用场景:RMQ 问题
ST 表(Sparse Table)最主要的应用就是查询给定区间 内的最大值或最小值。
- 特点:预处理时间复杂度为 ,查询时间复杂度为 。
- 适用性:适用于数据不会发生变化(静态),但查询次数极其频繁的场景。
2. ST 表能处理的具体问题类型
除了最基础的区间最大/最小值,ST 表还可以处理任何满足 “可重复贡献性” (Idempotent Property) 的运算。
所谓可重复贡献性,是指对两个相同的数值或区间进行重复运算,结果不变。即 。常见的包括:
- 区间最大值 / 最小值 (Max/Min):最经典用法。
- 区间最大公约数 (GCD):因为 。
- 区间按位或 (Bitwise OR):。
- 区间按位与 (Bitwise AND):。
注意:区间和(Sum)不适合用 ST 表处理,因为 。处理区间和通常使用前缀和或树状数组,因为它们能提供更好的空间效率或支持修改。
3. ST 表 vs 线段树
| 特性 | ST 表 (Sparse Table) | 线段树 (Segment Tree) |
|---|---|---|
| 预处理 | ||
| 查询 | ||
| 修改 | 不支持(或代价极大) | 支持 修改 |
| 空间 | ||
| 适用性 | 静态区间最值/GCD | 动态区间维护 |
实现
预处理
void ST_prework() {
for (int i = 1; i <= n; i++) f[i][0] = A[i];
int t = log(n) / log(2) + 1;
for (int j = 1; j < t; j++)
for (int i = 1; i <= n - (1 << j) + 1; i++)
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
查询
int ST_query(int l, int r) {
int k = log(r - l + 1) / log(2);
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
相关题目
例1. 与众不同
给出一个长度为 的序列 ,定义「完美序列」:一段连续的序列满足序列中的数互不相同。
现有 次询问,询问在区间 之间最长的完美序列长度。
预处理 start[] 数组
预处理好到每个位置 为止,最长完美序列的开始位置,记为 start[x]。
因为 和 之间的数字均不相同,且 对应的数字会和区间 之间的某个数字相同。若数字 上一次出现的位置为 lst[A[i]]。那么 。
下面是 start 数组的计算方法,其中 lst 数组的初始值为 0。数组从 开始编号。在计算 的值以后,我们同时更新了 的值。
start[i] = max{ start[i - 1], lst[A[i]] + 1};
lst[A[i]] = i;
处理查询
对于每个询问的区间 ,我们可以依次枚举每个位置 ,从而更新最长的完美序列长度。值得特别注意的是,start[x] 的值可能小于 ,此时最长完美序列的长度为 ,其他情况长度为 。每次询问的时间复杂度为 。
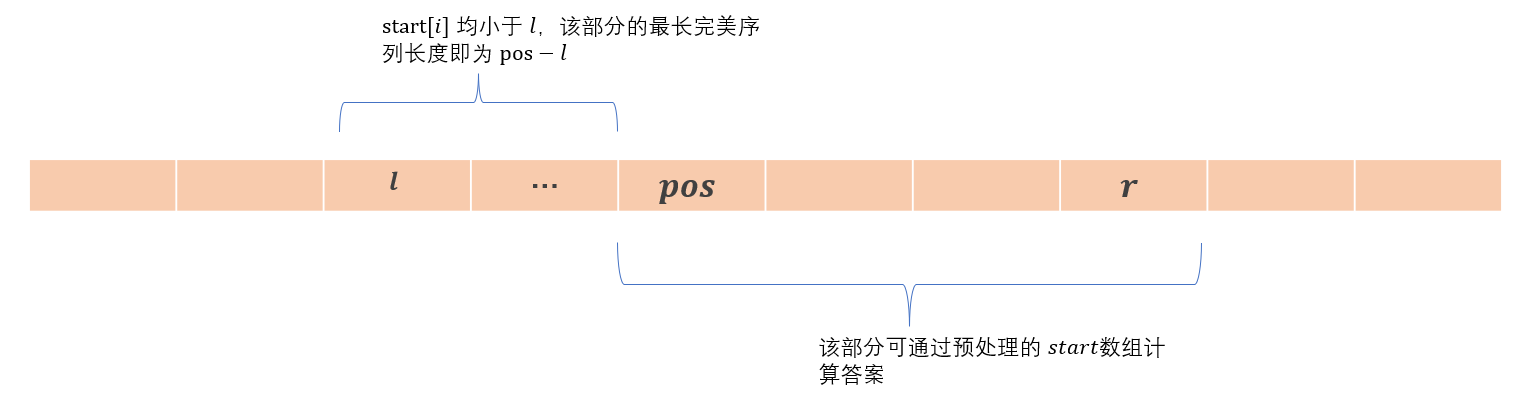
如何更快的计算出答案呢?本题寻找的是区间每个位置的最长完美序列的最大值,本来说区间最大值可以通过 ST 表维护,但本题询问的区间中有一部分位置对应的 start 值小于询问区间左端点。幸运的是,start 数组具有单调性,我们可以直接二分查找出第一个满足 位置 pos,该位置将区间分为了两部分,左边部分能够得到的最长完美序列即为 。而右边部分可通过 ST 表在 的时间计算出答案。每次询问,可以 的时间给出答案。
参考代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
int A[N], start[N], B[N];
int lst[N * 10];
int f[N][20];
int query(int l, int r) {
int ans = 0;
int pos = lower_bound(start + l, start + r + 1, l) - start;
ans = pos - l;
if (pos <= r) {
int t = log(r - pos + 1) / log(2);
ans = max(ans, max(f[pos][t], f[r - (1 << t) + 1][t]));
}
return ans;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> A[i], A[i] += 1e6;
for (int i = 1; i <= n; i++) {
start[i] = max(start[i - 1], lst[A[i]] + 1);
f[i][0] = i - start[i] + 1;
lst[A[i]] = i;
}
for (int j = 1; j <= 19; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
for (int i = 1; i <= m; i++) {
int l, r;
cin >> l >> r;
l++, r++;
cout << query(l, r) << "\n";
}
}